Sfasamento: Presa come riferimento la fase della tensione α, e confrontata con la fase delle corrente β si chiama sfasamento la differenza φ=α-β.
Fasore:con questo termine si indicherà la rappresentazione statica di tensioni e correnti che in regime sinusoidale risulterebbero sempre in movimento e quindi gestibili con calcoli piuttosto difficili di tipo trigonometrico o differenziale. Nel campo dei fasori vale un'algebra molto simile a quella vettoriale ma il cui campo di esistenza è quello dei numeri complessi.
Valore efficace:il valore efficace di una grandezza periodica è quell'equivalente valore di tensione continua che nello stesso tempo trasferirebbe sullo stesso carico resistivo la stessa quantità di calore per effetto joule. Se la grandezza in esame fosse sinusoidale allora l'estrazione del valore efficace dal valore di picco avviene semplicemente dividendo per la radice di due (non vale per una generica forma d'onda).
Valore di picco: Valore massimo positivo raggiunto da una funzione periodica, più intuitiva nelle funzioni sinusoidali in cui si può pensare facilmente anche alla grandezza picco picco, ovvero dal massimo positivo al minimo negativo. Dividendo la tensione di picco di una sinusoide per radice di due si ottiene il precedentemente detto valore efficace.
Strumenti a valore efficace: Ad esempio un normale tester o multimetro digitale se non diversamente indicato. Dato che non è possibile visualizzare un valore oscillante è necessario portare a display un valore stabile quale una media e/o un valore efficace. Dato che la media di una sinusoide è zero non ci sarebbe nessuna utilità di informazione quindi si mostra il valore efficace. Alcuni strumenti mostrano informazioni simili ma comunque chiaramente indicate di che tipo. alcuni strumenti portano la dicitura true RMS.
seno: dicasi seno dell'angolo alfa la proiezione del punto di intersezione del raggio rotante con la circonferenza goniometrica sull'asse delle ordinate (asse verticale). Dato che il raggio della circonferenza goniometrica è 1 metro per definizione, il valore del seno dell'angolo alfa corrisponderà ad un valore metrico compreso tra -1 e +1.
Calcolatrice consigliata:Per seguire meglio il video tutorial, o semplicemente per essere allineati con il metodo didattico presentato in questo articolo consiglio l'uso della calcolatrice "SHARP EL-506W" con oltre 490 funzioni. Esiste il modello write view che fornisce le stesse potenzialità di calcolo uguali con maggiore leggibilità a display. Ad ogni inizio di anno scolastico invito i mie allievi di fornirsi di questo strumento dato il basso costo, così che si procede meglio ai calcoli dato che seguiranno passo passo i tasti che l'insegnate digita durante le lezioni alla lavagna. Questo è il mio metodo didattico. M.G.
Corrente elettrica: Effetto delle cariche elettriche negative (elettroni) attraverso una sezione di un circuito. unità di misura ampère. si misura inserendo lo strumento in serie al punto di interesse, si deve quindi interrompere il circuito originale. per non perturbare la grandezza in esame la resistenza interna dello strumento deve quindi essere il più possibile prossima a zero.
Tensione elettrica. Effetto delle cariche accumulate tra due punti di un circuito. unità di misura volt. Si misura inserendo lo strumento in parallelo al punto interessato. per non perturbare la misura lo strumento deve avere una resistenza interna così alta da risultare paragonabile a infinito (circuito aperto). La tensione si differenzia dalla differenza di potenziale (d.d.p.) perché al contrario di questa è in grado di produrre del lavoro elettrico trasformando nel punto del circuito dell'energia.
Regie stazionario: Considerata una rete elettrica lineare (quando contiene solo generatori e resistori) o non lineare (quando contiene anche elementi che non rispondono direttamente a una legge volt-amperometrica lineare, come diodi condensatori, induttanze, transistor, ecc) il regime di funzionamento si dice stazionari se per ogni punto della rete le derivate della tensione e della corrente sono sempre nulle in ogni istante. In questo tipo di funzionamento le induttanze si comportano come dei corti circuito mentre le capacità come degli interruttori aperti. Alcuni componenti potranno essere assimilati a dei generatori ideali equivalenti di tensione e di corrente, si pensi ad esempio al diodo rettificatore al silicio 1N4007, quando è polarizzato diretto esso presenterà una caduta costante tra anodo e catodo detta "Vu-gamma" pari a 0,6 V che potrà essere sostituita con un equivalente generatore di tensione.
Regime periodico sinusoidale:si trova in questo regime una rete alimentata con uno o più generatori di corrente e di tensione in grado di imprimere una forma d'onda sinusoidale la quale generalmente non presenta lo stesso angolo (fase) in ogni lato del circuito. Sono più facilmente studiabili le reti sinusoidali così dette "isofrequenziali", ovvero quelle in cui tutti i generatori operano con la stessa pulsazione angolare della forma d'onda impressa. Dobbiamo prestare attenzione ad alcuni componenti che in regime stazionario sono "corti" o "aperti" come le induttanze e i condensatori, perché in questo caso assumeranno un comportamento ohmico, quindi conducono, in maniera proporzionale non solo al proprio valore in Farads o Henry, ma anche alla pulsazione angolare omega della tensione ad essi applicati. Con le trasformazioni fasoriali si può comunque linearizzarne il comportamento e rendere applicabili le normali leggi e teoremi del regime stazionario.
Regime variabile: È il più complesso da studiare perché studia la razione della rete e dei singoli componenti durante le variazioni di regime come avviene ad esempio durante le chiusure e aperture degli interruttori o rotture di specifiche parti della rete. Lo studio si effettua tramite le "equazioni differenziali" e si svolge su tre diversi istanti, prima della manovra, durante la manovra, dopo la manovra. È disponibile una dispensina manoscritta nei link verso fine pagina. Esiste una tecnica di linearizzazione delle reti in regime transitorio che impiega le Laplace trasformate. queste al contrario di quanto si crede, semplificano i calcoli dato che trasformano operazioni integro differenziali in divisioni e prodotti rispettivamente. Le Laplace trasformate sono tabellate e scaricabili da internet. seguite questo link per scaricare i teoremi sulle L-Trasformate www.gtronic.it/energiaingioco/it/scienza/dispense_pdf/Teoremi%20Laplace%20Trasformate.pdf
Convenzione dei generatori e degli utilizzatori.
Consideriamo un generico bipolo elettrico (componente a due fili), si fissi il riferimento per la tensione. Se, una volta inserito il componente in uno specifico ramo del circuito, la corrente risulta entrante dal morsetto positivo il bipolo è convenzionato da utilizzatore, se invece la corrente risulta uscente dal polo positivo allora il medesimo bipolo è convenzionato a generatore. nota bene, un generatore propriamente detto può essere convenzionato da utilizzatore, si pensi ad esempio alla batteria del telefonino quando questo è sotto carica. Un bipolo resistore è sempre convenzionato da utilizzatore, infatti in esso vale la legge di ohm e si misurerà con il positivo nel punto di entrata della corrente. Per quanto riguarda la potenza di un generatore di tensione, questa risulterà fornita (o erogata) se il generatore è convenzionato da generatore, risulterà dissipata se il generatore è covenzionato da utilizzatore. Una resistenza dissipa sempre potenza.
Potenza.
La potenza in continua è data da una delle tre formule P=V*I, P=R*I^2, P=V^2/R, ed ha sempre unità di misura Watt.
In alternata si distingue tra potenza attiva, reattiva, apparente. Dato il vettore della potenza complessa, si ottiene la potenza attiva proiettandolo sull'asse delle ascisse, ovvero W= V*I *cosφ, e si ottiene la potenza reattiva proiettandolo nell'asse delle ordinate V.A.R. = V*I*sinφ. La potenza apparente rimane solamente V*I con unità di misura Volt-Ampere.
Numeri complessi: il campo dei numeri complessi risulta isomorfo (stessa forma) al piano cartesiano ma ha alcune importanti proprietà. I suoi elementi si chiamano numeri complessi e sono stati ripresi pari pari nello studio dei fenomeni elettrici sinusoidali introducendo una enorme semplificazione di calcolo. È indispensabile conoscere alcune proprietà fondamentali, queste sono:
- Il piano complesso è formato da un asse orizzontale, detto reale, e da uno verticale detto immaginario.
- I numeri complessi sono coppie di valori, il primo si trova sull'asse reale il secondo su quello verticale detto immaginario.
- I numeri complessi operano nel piano complesso che viene definito "campo complesso". ogni elemento del piano complesso è un numero complesso ma dal punto di vista elettrico/elettronico sarà inteso come fasore (se tensione o corrente) o operatore complesso (se impedenza). I fasori sono indicati con il segno di vettore oppure una barretta sopra al nome (in caso di difficoltà grafica semplicemente si scrive in stampatello e usando il grassetto) mentre l'operatore complesso ha semplicemente un puntino. Ne consegue che una zeta maiuscola stampatello con il puntino sopra rappresenta l'impedenza.
- il modulo di un numero complesso è l'applicazione del teorema di Pitagora sulle sue componenti e rappresenta la distanza della punta del vettore con l'origine. essendo una distanza è sempre positivo.
- Il simbolo "i" o "j" non è un numero ma il cosiddetto coefficiente dell'immaginario, vale infatti i^2=-1 questo giustifica il nome "dell'immaginario" dato che non esiste alcun numero che elevato al quadrato dia un valore negativo. L'introduzione del coefficiente "i" rende possibile, in campo complesso, l'estrazione delle radici quadrate di numeri negativi, cosa impossibile in campo reale.
- La somma di due numeri complessi si esegue per componenti. es: C1=(2+i1) C2=(-1+3i) C1+C2=(1+i4)
- La differenza si esegue concettualmente come la somma.
- Il coniugato di un numero complesso è quel numero (in elettronica/elettrotecnica fasore, specialmente di corrente in fase di calcolo delle potenze) che ha la stessa parte reale ma parte immaginaria invertita di segno. secondo questa definizione, dati i fasori di tensione e di corrente V=(30+i20) e I=(2-i1) la potenza complessa sul componente interessato da questi parametri vale V I~ (ho indicato il coniugato con il tilde per difficoltà grafica, di solito ha una piccola v sopra la testa). quindi calcoliamo il valore della potenza complessa eseguendo il calcolo V I~=(30+i20)*(2+1i)= (30*2)+(30*i1)+(i20*2)+(i20*i1)=60+30i+40i-20 si sommano ora tra di loro le parti reali e le parti immaginarie (quelle con la i) e si ottiene S=(40+70i) (con S si indica solitamente la potenza complessa). Ora, la parte senza la i (parte reale) si chiama potenza attiva e si misura in Watt, mentre la parte con la i (parte immaginaria) viene privata del termine i e rappresenta la potenza reattiva e si misura in VAR (volt ampere reattivi). Il componente dell'esempio sta quindi assorbendo o generando (dipende dal circuito) una potenza attiva di 40 watt e una potenza reattiva di 70 VAR. (questa e, una delle cose più importanti).
- Rapporto tra numeri complessi: è un'operazione molto importante perché nel nostro ambito permetterà l'applicazione della legge di ohm. La divisione tra numeri complessi si ottiene moltiplicando entrambi il numeratore e il denominatore per il complesso coniugato del denominatore. Il risultato è generalmente un numero complesso.
- prodotto di numeri complessi:è in generale un numero complesso e si esegue con le stesse regole del prodotto di due binomi con l'avvertenza che il coefficiente dell'immaginario J moltiplicato per se se stesso da come risultato -1.
- Esiste la possibilità di estrarre le radici dei numeri complessi ma capiterà di raro nei normali calcoli di dimensionamento.
- Se usate la calcolatrice consigliata in questo tutorial "sharp EL-506 a 494 funzioni", si entra in campo complesso agendo sul tasto "mode" e digitando 3. In alto a sinistra del display comparirà "xy" che indica che ci troviamo nelle coordinate rettangolari del piano complesso. Possiamo ora inserire i complessi esattamente come li leggiamo ed eseguire qualsiasi operazione.
Iniziamo il nostro tutorial di elettrotecnica.
Cominciamo con l'esporre i principali teoremi e principi esponendone l'enunciato, mostrandone degli esempi e dimostrandone l'utilità in ambito elettronico. Questi sono:
- Legge di Ohm
- principio dei generatori reali equivalenti
- principio di sovrapposizione
- primo principio di Kirchhoff
- secondo principio di Kirchhoff
- teorema di Thévenin
- teorema di Norton
- teorema di Tellegen
- Teorema di Boucherot.
Legge di ohm.
Il promemoria che fornisco sempre ai miei più giovani allievi è di ricordare la frase "Viva la Repubblica Italiana", le iniziali rappresentano l'equazione V=R*I Dal punto di vista più tecnico la legge di ohm è una equazione di primo grado che stabilisce una relazione lineare (rappresentabile con una retta) tra le due grandezze fondamentali dell'elettrotecnica/elettronica, ovvero la tensione e la corrente. Questa legge definisce un nuovo elemento fisico chiamato Resistenza pari al rapporto della tensione applicata ai capi di un bipolo e la corrente che lo attraversa. Se la legge volt/amperometrica se ne ricava tracciando un grafico per punti risulta lineare allora il bipolo in esame è una resistenza propriamente detta. Questa legge definisce inoltre che il rapporto tra le unità di misura Volt e corrente "I" definisce, in caso di proporzionalità lineare, una nuova unità di misura detta appunto Resistenza.
Esiste un'altra forma della legge di Ohm che mette in relazione la sezione del conduttore soggetto all'applicazione della tensione che comporta il transito della corrente, con la lunghezza del conduttore stesso. Esiste un altro parametro, tipico del materiale di cui si compone il conduttore, chiamato "ρ", che è specifico di ogni elemento della tabella periodica. L'enunciato di questa seconda forma della legge di Ohm recita: La resistenza "R" di un conduttore è direttamente proporzionale alla sua Lunghezza moltiplicata per la resistività ρ ed inversamente proporzionale alla sezione del conduttore stesso. in formula si veda la foto sottostante: Attenzione: L'uso della carta e penna e riprese fotografiche sono volute a titolo sperimentale e al fine di dare un tocco di originalità alla pubblicazione visto che porterà con se la calligrafia dell'autore.
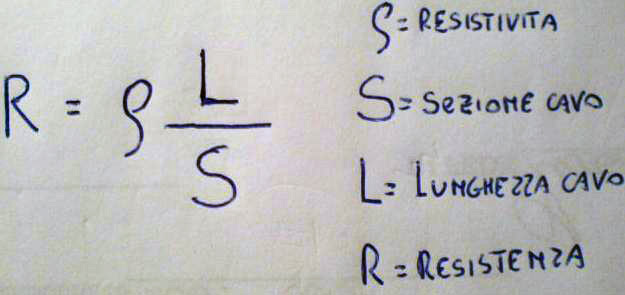
L'unità di misura è appunto l'ohm sia nella prima forma che nella seconda forma. Esiste una ulteriore forma della medesima legge applicata però ai fasori e quindi al campo dei numeri complessi. Se si parla di fasori significa che la rete elettrica o la parte del circuito elettronico in esame è soggetto a un regime periodico e presumibilmente sinusoidale. Vediamo subito un esempio facendo un semplice esercizio, in cui i bipoli si suppongono già trasformati in fasori e impedenze. (vedi numeri complessi a glossario)
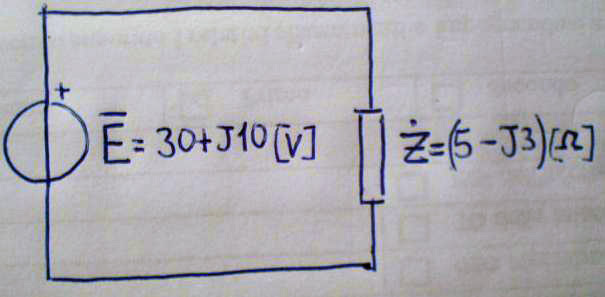
Procediamo allo svolgimento dei calcoli dopo avere messo la legge di ohm nella sua forma di rapporto delle grandezze tensione su impedenza. Stiamo quindi cercando la corrente complessa che circola nel circuito.

nello svolgimento di questo esercizio non si è fatto alcun riferimento alla provenienza dell'impedenza, essa potrebbe essere anche la sintesi di una rete molto complessa di induttori, capacità e resistenze che per successivi calcoli di "serie" e "parallelo" si sono ridotti a un unico bipolo impedenza con un valore complesso equivalente in ohm. Nulla si è detta anche sulla frequenza di funzionamento della rete dato che sia i generatori che i vari bipoli sono già stati trasformati in fasori e sintetizzati in soli due elementi equivalenti.
Tornando al bipolo resistivo propriamente detto, in elettrotecnica può essere ben diverso dalla forma che si attende un elettronico dato che potrebbe trattarsi semplicemente si un filo di varia lega, ad esempio constatana, o altre adatta a fare filamenti per la trasformazione termica in phon, tostapane, stufe elettriche ecc. Oppure, in maniera più robusta, serpentine all'interno di boiler, o candelette per i motori diesel. Per noi elettronici hanno comunque un aspetto molto familiare, ovvero un cilindretto verniciato con delle belle righette colorate che ne rappresentano il valore secondo il noto codice colori:

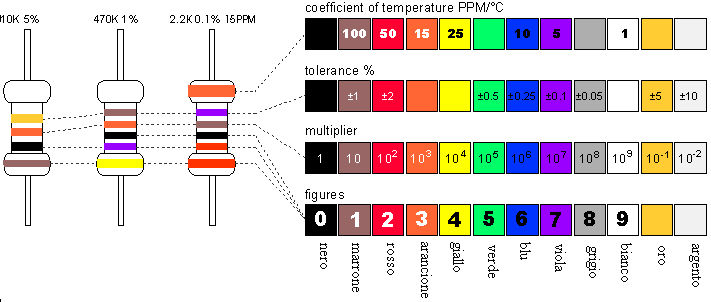
Come esercizio si provi ad associare il valore a queste due resistenze:


Un altro importantissimo parametro delle resistenze reali è la dimensione del loro corpo in quanto è grosso modo proporzionale alla potenza che esse sono in grado di dissipare per effetto joule senza incendiarsi o anche semplicemente surriscaldarsi perdendo con buona probabilità la precisione costruttiva in ohm segnata nel codice colori. Insomma una resistenza che per qualche ragione avesse fumato un po' ma non risulta interrotta è bene sostituirla perché probabilmente non ha più il valore indicato, in una applicazione audio un lieve danno potrebbe renderla ad esempio più rumorosa o in uno strumento di misura comprometterne la precisione.
Ma dal punto di vista pratico, cosa è una resistenza? Come si costruisce?
Quelle più comuni, che vede nelle figure sovrastanti sono ottenute tramite una lega binaria, in cui due metalli con specifica e diversa ρ vengono miscelati assieme con precise percentuali di uno nell'altro allo scopo di ottenere un cilindretto omogeneo del valore in ohm desiderato. Questo è possibile perché le leghe binarie hanno un grafico della ρ risultante fortemente non lineare come quello che vedete nella figura:
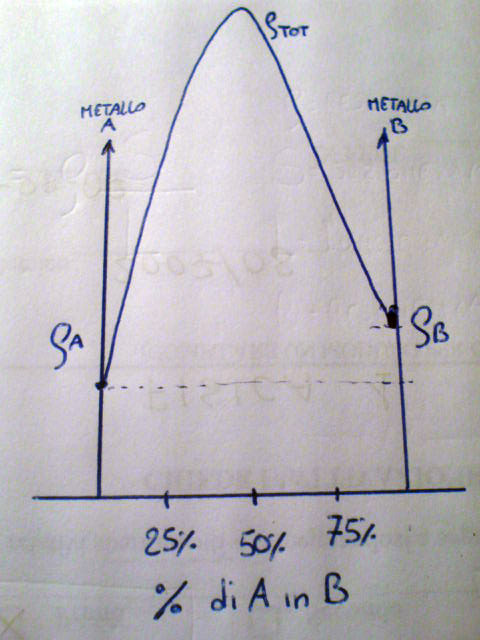
Per questioni grafiche la campana non può essere disegnata molto più alta e stretta, come è nella realtà. È grazie alla forma di questa campana che si possono ottenere in pochi millimetri cubici resistenze elevatissime nell'ordine dei mega ohm, come anche , nello stesso volume resistenze di pochi ohm o addirittura frazioni di ohm, tutto sta nel "giocare correttamente nella percentuale del metallo A rispetto a B nella lega binaria. Importante è notare che i due valori ρ non possono stare alla stessa altezza, difatti se così fosse si tratterebbe dello stesso metallo e la campana non si formerebbe, al suo posto ci sarebbe una linea ad altezza costante che unisce il lato sinistro con quello destro e non si avrebbe alcun controllo sul valore finale della resistenza tramite la percentuale del metallo A in lega con B. Nella prossima foto vediamo la struttura meccanica della resistenza.
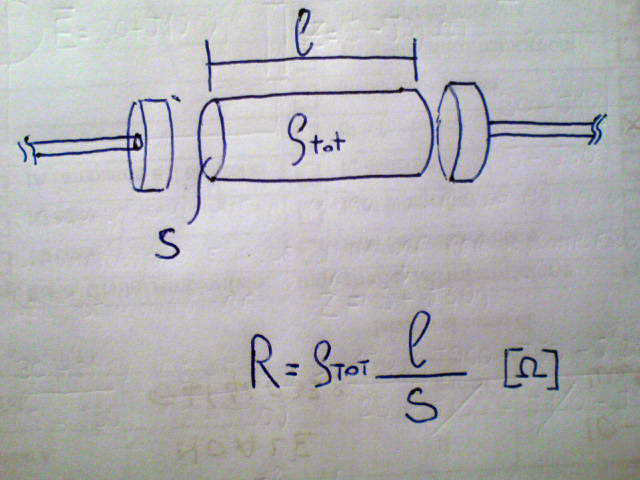
Il cilindretto metallico ottenuto tramite lega binaria "tarata" ha un valore ohmico ben preciso, nei casi standard non differisce generalmente più di +/- 5% dall'indicato o anche meno, spesso 1%. Esso viene connesso tramite due cappuccetti metallici a cui sono saldati i reofori al circuito elettrico/elettronico esterno. La struttura così ottenuta viene di solito ricoperta di ceramica o altro materiale vetroso su cui successivamente vengono dipinte le fascette del codice colori. Tecnicamente parlando la costruzione di un componete smd (surface mounting device) non è molto diversa da quella esposta.
È importante ricordare che in ogni caso una resistenza dissipa sempre potenza attiva.
Vediamo alcune importanti applicazioni della legge di ohm per l'elettronica.
Come è noto gli amplificatori operazionali sono costruiti in modo da non permettere l'ingresso della corrente sui loro pin invertente e non invertente. Supponiamo di avere un circuito in catena aperta come quello in figura che è notoriamente un comparatore, ovvero porterà l'uscita alta (a meno delle cadute interne pari a circa 1,4 volt tenderà alla tensione di alimentazione Vcc) quando la tensione all'ingresso non invertente sarà maggiore di quella all'ingresso invertente.
Questo comparatore dunque esegue il ragionamento: if (V- > V+) Then (Vo = gnd) else Vo= (Vcc-1,4v)
supponiamo che l'ingresso non invertente sia collegato a un sensore di temperatura o luminosità o qualsivoglia grandezza tradotta in volt, mentre l'ingresso invertente sia collegato al punto centrale della serie di due resistenze di valore R1=4,7k e R2=680 ohm. Ci si chiede, a che valore trasdotto in volt della grandezza esterna si accenderà il LED in uscita? Quanto vale la resistenza sul LED se esso è costruito per accendersi correttamente con 1 mA e ha una caduta anodo catodo è di 1,5 volt?
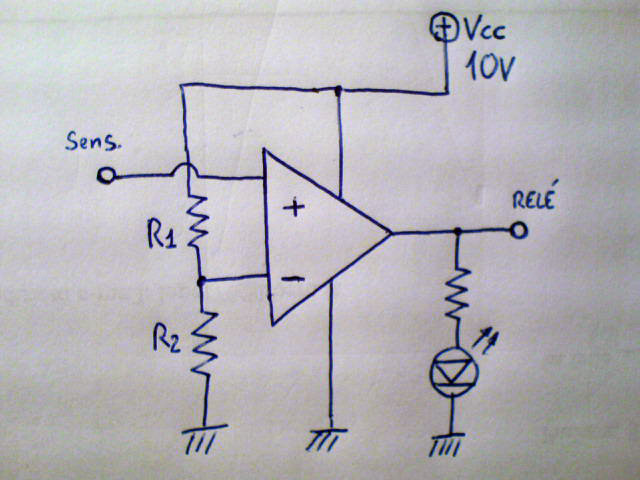
Questo circuito contiene ben 3 applicazioni della legge di ohm, due per risolvere il partitore di tensione all'ingresso e una per il calcolo della resistenza generalmente indicata con Rd che sta in serie al LED. Vediamo come mai la nota formula del partitore di tensione si può ottenere tramite una doppia applicazione della legge di ohm con il vantaggio di non dover ricordare la formula.
- applichiamo la legge di ohm sulla resistenza equivalente alla serie, cioè R1+R2, otteniamo la corrente totale.
- dalla def. di serie questa attraversa sia R1 che R2.
- moltiplichiamola per R2 e troviamo quindi la tensione tra massa e il morsetto invertente (punto di scatto).

.Ora ricaviamo la formula del partitore di tensione facendo una doppia applicazione della LEGGE DI OHM.

Per quanto riguarda la resistenza di uscita in serie a LED procediamo così:
- sostituire l'uscita alta dell'operazionale con un equivalente generatore di tensione pari a Vout=10-1,4=8,6 volt.
- sostituire il LED con un generatore di tensione equivalente alla sua caduta costante pari a 1,5 volt
- sottrarre a Vout il generatore equivalente del led Vr=8,6-1,5=7.1 volt
- applicare la legge di ohm trovando il valore della Rd sapendo che deve circolare 1mA

Una volta scelta la resistenza di serie più vicina al valore calcolato è bene riapplicare la legge di ohm e verificare nuovamente la corrente per vedere se il nuovo valore è accettabile in quel punto del circuito. La legge i ohm è una delle formule più usate in ambito elettrico/elettronico.
Completo l'esposizione del partitore di tensione dando un utile promemoria: La tensione di uscita Vo del partitore è uguale alla tensione applicata al partitore Vi diviso la somma delle due o più resistenze del partitore moltiplicato per la resistenza a cui capi prelevo la tensione Vo.
Esiste la possibilità di ripartire la corrente anziché la tensione, lo schema è costituito da due resistenze connesse a un nodo. Si presume che al nodo entri una certa corrente "J". La corrente su una delle due resistenze si calcola dividendo la corrente entrante "J" per la somma delle due resistenze, e moltiplicando il risultato per la resistenza non interessata dal passaggio della corrente che sto cercando (l'altro lato). il concetto si può facilmente estendere a un partitore di corrente costituito da più resistenze in parallelo purché nella fase di moltiplicazione lo si faccia per la resistenza equivalente del ramo non interessato al passaggio svolgendo tutti gli eventuali serie-parallelo di resistori visti da quel punto in poi. Comunque si tratta di una doppia applicazione della legge di ohm.
Principio dei generatori equivalenti.
Se consideriamo un regime stazionario, esistono 4 tipi di generatori, essi sono:
- generatore ideale di tensione
- generatore ideale di corrente
- generatore reale di tensione
- generatore reale di corrente
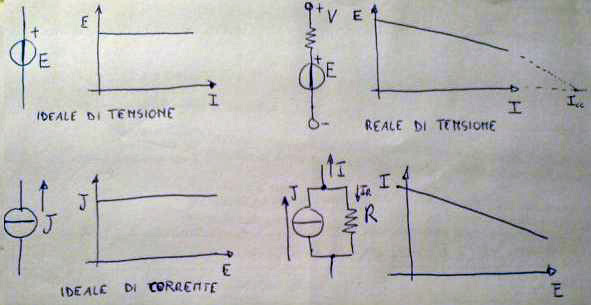
Nel generatore reale di tensione, la V risultante ai morsetti esterni è data dalla somma algebrica delle tensioni impressa E del generatore ideale interno meno la caduta hommica I*R simula resistenza interna. Ne consegue che la tensione esterna V dipende dal grado di carico del generatore reale, ovvero da quanta tensione cade internamente sulla R a causa della maggiore corrente richiesta verso il carico esterno, quindi la curva volt - amperometrica ha l'aspetto di una retta con pendenza negativa che incrocerà l'ascissa (asse orizzontale in corrispondenza della corrente di corto circuito Icc.
Nel generatore reale di corrente di applichi invece il primo principio di Kirchhoff al nodo interno per definire quanta corrente potrà fluire sui morsetti esterni verso il carico.
Alcuni metodi risolutivi delle reti elettriche/elettroniche prevedono che e zone in cui si opera siano costituiti da solo generatori reali di tensione o generatori reali di corrente, questi sono ad esempio il metodo delle correnti di maglia (esposto più avanti) o il metodo dei potenziali ai nodi. Se la rete iniziale non è conforme a quanto detto, va prima adeguata trasformando i generatori reali di tensione in reali di corrente o viceversa a seconda del caso.
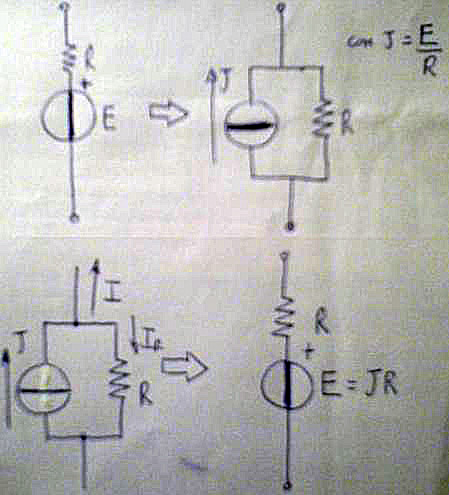
La rete ottenuta si chiama rete adeguata e dal punto di vista elettrico è equivalente a quella originale, tranne per la questione energetica dove invece si deve tornare alla rete originale per il calcolo ad esempio di potenze e energie.
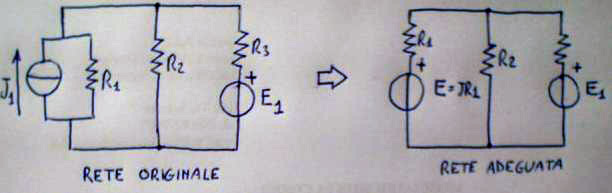
dopo avere eseguito questo passaggio sarà possibile applicare il metodo delle correnti di maglia (o delle correnti di anello) che viene presentato più avanti. Dal punto di vista elettronico una situazione analoga la possiamo incontrare in qualche rete posta davanti a un amplificatore operazionale che per le sue caratteristiche bufferizza, ovvero rende considerabile isolatamente un particolare circuito (ad esempio un filtro o altro) posto davanti a uno solo dei suoi morsetti di ingresso, ad esempio l'ingresso non invertente.
Principio di sovrapposizione.
Si consideri una rete elettrica o elettronica che contenga solo componenti lineari, ovvero generatori reali o equivalenti e resistori. Si consideri una "porta" ovvero due morsetti. o due punti del circuito su cui si vuole stimare l'effetto complessivo di tutti i componenti presenti nella rete. Tale effetto sarà uguale alla somma dei singoli effetti ottenuti facendo agire i generatori presenti una alla volta. Fare "agire" i generatori significa permettergli di imprimere la loro grandezza elettrica sia essa una corrente o una tensione. Per non fargli agire, ovvero spegnerli sulla carta si può usare il trucco di eliminare il cerchietto dal disegno del generatore. Automaticamente scopriremo che le barrette contenute nei singoli mettono in c.c. i generatori di tensione (fanno imprimere quindi tensione nulla) e aprono i rami in cui sono inseriti i generatori di corrente (fanno imprimere corrente nulla). Lasciamo agire i generatori una alla volta calcolando per ognuno di essi la tensione alla porta considerata. atterremo tante tensioni parziali quanti sono i generatori della rete. sommiamo infine tutte queste tensioni e otterremo la tensione che è presente in quella specifica porta con tutti i generatori in azione. nota bene: se si cambia porta elettrica tutti i calcoli vanno ripetuti.
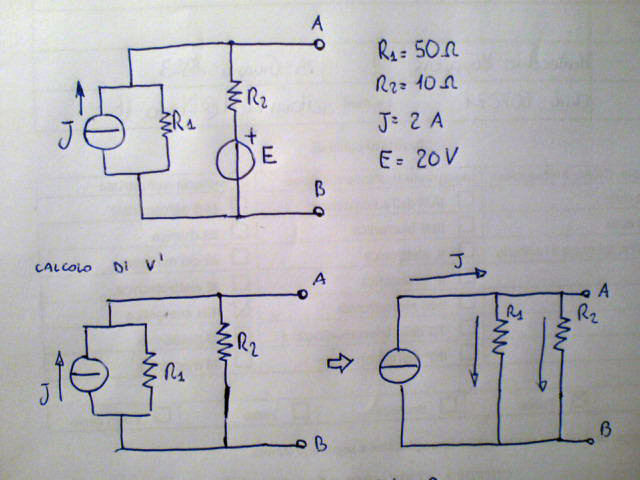
nel primo disegno c'è la rete originale composta da due generatori reali, uno di corrente e uno di tensione. Il metodo prevede che agiscano una alla volta sulla porta elettrica prescelta, ovvero i morsetti AB. iniziamo togliendo il cerchietto al generatore di tensione, si vede facilmente che esso diventa un corto circuito tra i suoi morsetti, ovvero imprime tensione nulla. La rete risultante contiene solo un generatore i corrente e il resto del circuito resistivo costituisce un partitore di corrente. Seguono i semplici calcoli.

Trovata la corrente sulla resistenza in parallelo alla porta AB applichiamo la legge di ohm e troviamo la prima tensione.
Ora dobbiamo fare agire solo il secondo generatore, durante questa fase il generatore di corrente si apre come si vede facilmente togliendogli il cerchietto. Togliere il cerchietto equivale a fargli imprimere una corrente nulla.
Otteniamo un circuito che è palesemente un partitore di tensione.
Troviamo con i semplici passaggi indicati nella foto la seconda tensione parziale.
Sommiamo infine le due tensioni parziali "sovrapponiamo gli effetti" ed otteniamo l'effetto complessivo sulla porta desiderata.
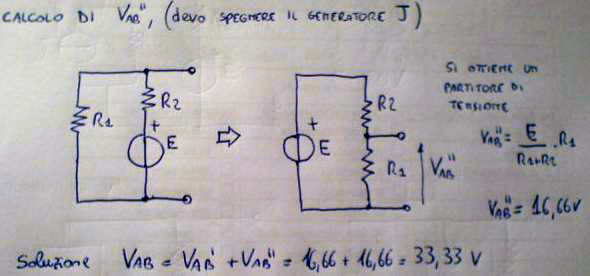
Questo metodo vale solo sulle reti così dette lineari.
Primo principio di Kirchhoff.
Questo principio, detto anche delle correnti ai nodi è molto utile in tantissimi ambiti elettronici, citandone uno, si pensi alla rete passiva posta davanti all'ingresso non invertente di un filtro butterworth del secondo ordine. Tale filtro possiede due nodi e una doppia retroazione. L'analisi di quel circuito avviene studiando prima un nodo e pio l'altro secondo questo primo principio di Kirchhoff.
L'enunciato afferma che la somma algebrica delle correnti in un nodo e pari a zero.

Consideriamo un generico nodo elettrico che abbia un qualsivoglia numero di rami confluenti, in questo esempio per semplicità solo 4. In questi rami le correnti siano indicate con un verso arbitrario. Siamo noti i valori di tutte le correnti tramite una unica incognita che vogliamo determinare con questo principio. Il calcolo ci restituirà non solo il valore ma anche il verso entrante o uscente a seconda del segno concorde o opposto a quello fissato inizialmente.
Indichiamo le correnti con I1,I2,I3,Ix e abbiniamoci il verso presunto e il loro valore tranne per Ix per la quale si indica solo un verso "supposto".
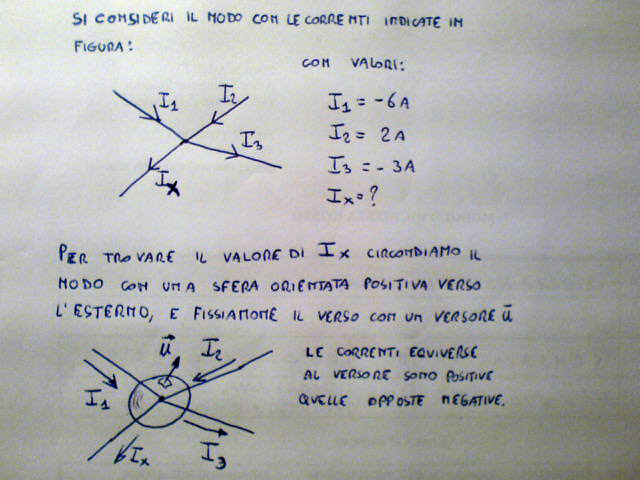
La sfera ipotetica con cui si circondata il nodo è noto come "insieme di taglio" e su di esso vale il principio di continuità, ovvero tutte le cariche che entrano devono anche uscire, sarebbe come dire che non disperde cariche in maniera misteriosa. Lo possiamo pensare come una espansione del nodo. Nei circuiti elettronici gli insiemi di taglio possono comprendere addirittura un "sottocircuito" identificabile nella scheda elettronica, con quanti componenti si vuole contenuti in esso, ma che rispettino sempre il principio di continuità. Le correnti che figurano equiverse al versore le scriviamo con il segno positivo, quelle discordi negativo. Facciamo attenzione che è importante scrivere sempre con le parentesi in modo che in un secondo passaggi possiamo inserire i valori algebrici con il segno dato. guardiamo la prossima foto.

Ora manca un ultimo semplice passaggio, eseguiamo la somma algebrica al membro di sinistra ottenendo -1. successivamente cambiamo i segni di ambo i membri dell'equazione giungendo al risultato finale.
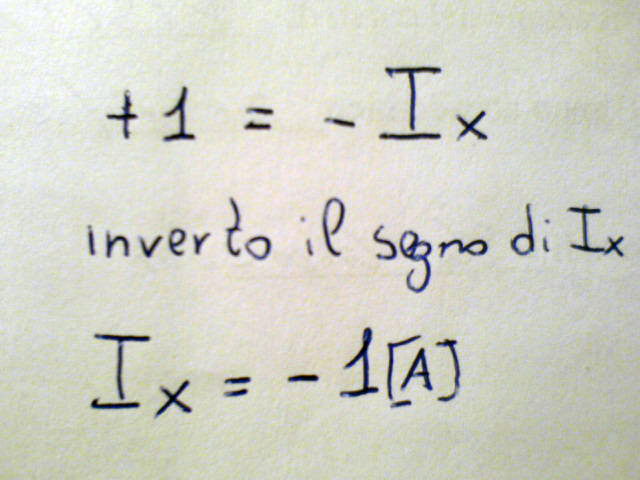
Anche in quei casi, in cui può sembrare banale la soluzione, sconsiglio di tentare una soluzione mentale perché più semplice il calcolo e più potrà essere imbarazzante un eventuale banale errore di calcolo. errare humanum est.
Consideriamo il filtro butterworth del secondo ordine visibile in figura:
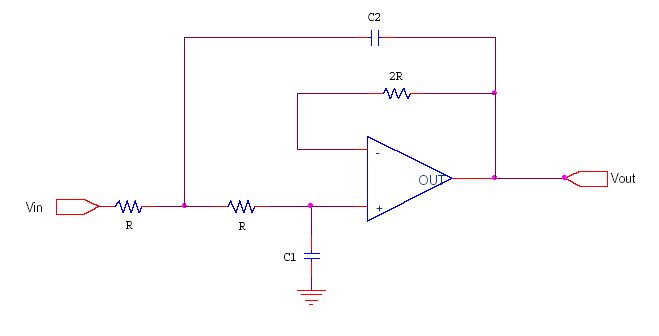
Salta subito all'occhio la presenza del nodo tra le due R nel circuito di ingresso. proviamo per esercizio ad applicare a tale nodo il principio di Kirchhoff ottenendo un'equazione simile a quella esposta in precedenza. Chi conosce i diagrammi di Bode provi a tracciare il diagramma del modulo e si accorgerà che tale filtro taglia con una pendenza di 40 db ogni decade.
Secondo principio di Kirchhoff.
Detto anche delle tensioni alle maglie, afferma che la somma algebrica delle tensioni in una maglia è pari a zero. Questo permette di determinare il valore di un generatore (o di un generatore equivalente di tensione) rimasto incognito.
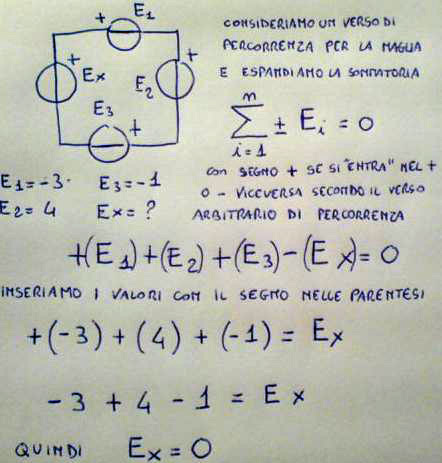
Varianti di questo principio, più e meno evidenti si applicano molto spesso. Si può considerare una variante di questo principio anche lo studio della maglia di ingresso di un BJT, nel momento in cui si consideri la resistenza di base attraversata dalla corrente di base Ib come un generatore stazionario equivalente, come anche lo sia la giunzione Vbe, pari alla V-gamma di un diodo polarizzato direttamente. Vediamo un semplice esempio:
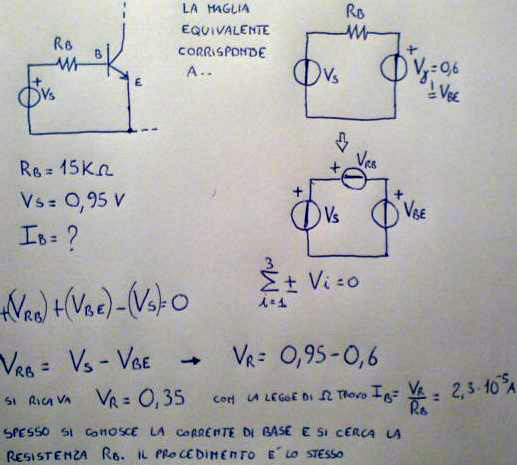
In ambito elettronico ci sono moltissime occasioni di applicazione di questo principio, lo applichiamo molte volte anche se spesso non ce ne rendiamo conto.
Teorema di Thévenin.
Al contrario di quel che si crede, si pronuncia esattamente come si scrive, date le origine dello scienziato a cui lo si attribuisce, un po' alla stessa maniera di come non si dice "jaul" ma "Jul" con riferimento al teorema di "joule".
Una rete elettrica lineare, per quanto complessa, è sempre riconducibile a un equivalente generatore ideale di tensione pari alla tensione a vuoto misurata alla porta in esame con in serie una resistenza pari alla totale resistenza della rete resa passiva vista dalla stessa porta. Vediamo un esempio nella semplice rete qui sotto in cui si è scelta la coppia di morsetti A-B come porta elettrica.
esempio: sia data la rete lineare in figura composta da un solo generatore di corrente e uno di tensione. Nella rete vi siano anche le resistenza R1 e R2 disposte come da schema.
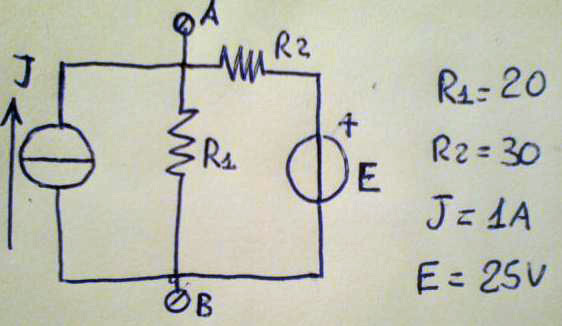
Applichiamo il teorema di Thévenin dapprima rendendo passiva la rete e trovando la resistenza equivalente vista dalla porta A-B, questa operazione si ottiene spegnendo i generatori, manovra che si esegue nella carta semplicemente togliendo i cerchietti dal disegno.
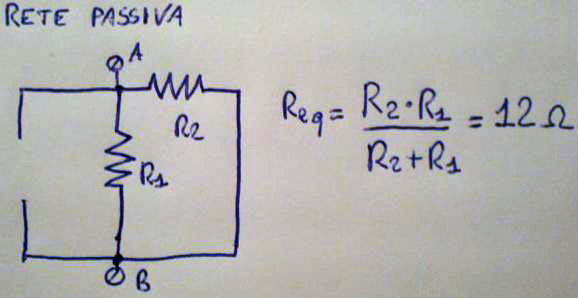
Si nota facilmente che per trovare il valore resistivo alla porta A-B è sufficiente eseguire il parallelo delle due resistenze.
Poi applichiamo il principio di sovrapposizione degli effetti facendo agire un generatore alla volta e calcolandone la tensione alla medesima porta A-B.
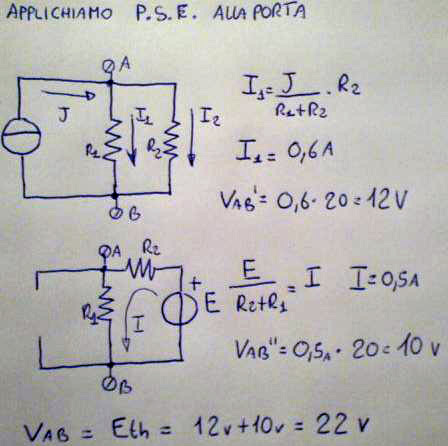
La somma degli effetti alla porta vale 22Volt, mentre le resistenza equivalente delle rate passiva vale 12 ohm, non ci resta che disegnare il generatore di tensione equivalente secondo Thévenin.
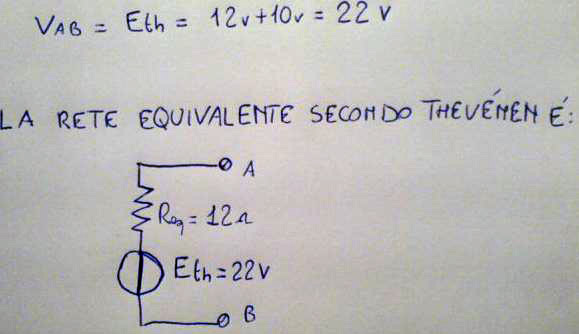
Il problema è quindi risolto dal punto visto di vista elettrotecnico. Ma vediamo un esempio applicato direttamente all'elettronica. Si abbia da calcolare la rete di polarizzazione del BJT mostrato nello schema sottostante.
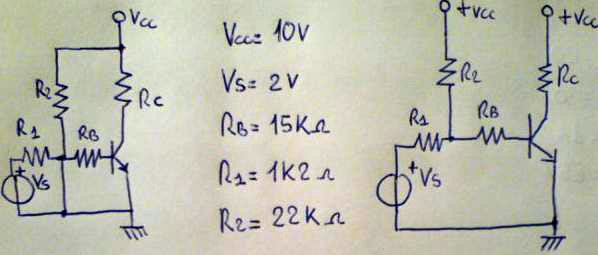
Applichiamo Thévenin alle maglie di ingresso esattamente come fatto precedentemente nell'esempio puramente elettrotecnico, ovvero, dopo aver isolato la rete che ci interessa sintetizzare nel generatore reale equivalente di Thévenin, ovvero aver trovato la porta A-B, rendiamo passiva la rete e ne calcoliamo la resistenza equivalente.
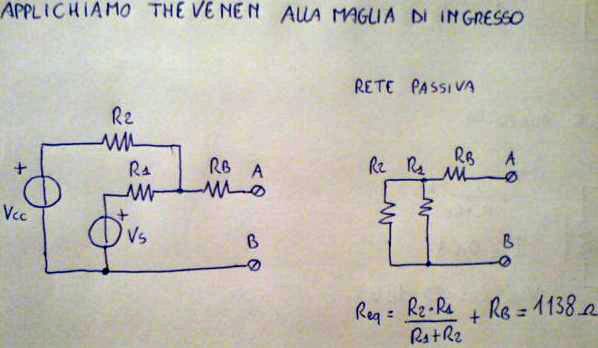
Ora procediamo applicando il principio di sovrapposizione degli effetti (P.S.E.),spegnendo i generatori uno alla volta. e sommandone gli effetti alla porta identificata.
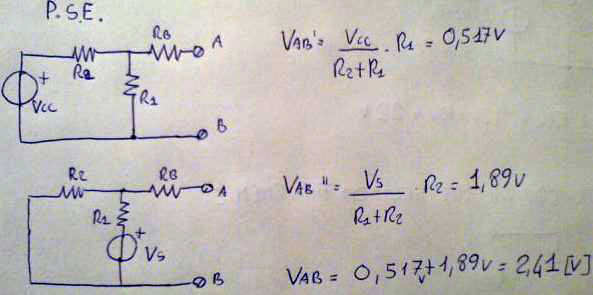
possiamo quindi sostituire l'insieme delle maglie con un unico generatore equivalente secondo Thévenin allo scopo di calcolare più agevolmente la corrente di base e quindi il punto di lavoro del BJT. si ottiene una resistenza equivalente pari a 1138 ohm (se si dovesse realizzare la rete e non solo usare il teorema per agevolare il calcolo della polarizzazione si arrotonda a 1k2, e un generatore equivalente di 2,41 volt).
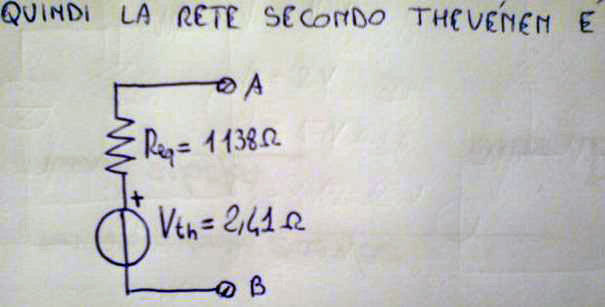
Questa "maglia" semplificata sarà equivalente ai fini della polarizzazione di base alla maglia precedente, e quindi potrà essere sostituita all'insieme delle maglie precedenti come vediamo nella prossima immagine.
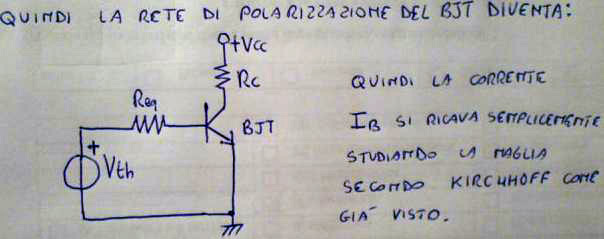
L'applicazione di questo teorema è tanto più vantaggiosa quanto più complessa è la rete che sta davanti al BJT. È inutile dire che questo è solo un esempio e che il metodo può essere applicato a una grande moltitudine di casi. È sicuramente più ovvio da applicare in quei casi in cui si entra direttamente in morsetti invertenti o non invertenti di operazionali che bufferizzano il segnale.
Teorema di Norton.
È il "duale" del teorema di Thévenin, ovvero si deve sostituire la frase "tensione a vuoto" con la frase"corrente di corto circuito" e la frase "alla porta A-B" con la frase "nel ramo" o "nel lato". il procedimento è analogo, ovvero si rende prima passiva la rete e se ne calcola la resistenza equivalente sul ramo momentaneamente aperto, successivamente si calcola la sovrapposizione degli effetti nel punto di interesse. Se ne ricava un equivalente generatore ideale di corrente che imprime la corrente di corto circuito "J di Norton" con in parallelo la resistenza equivalente della rete resa passiva. In definitiva si ha quindi un generatore di corrente reale data la presenza in parallelo di questa Requ .
Teorema di Telleghen.
Noto in bibliografia come teorema delle potenze virtuali, esso afferma che una volta convenzionato i bipoli tutti alla stessa maniera, ovvero o come generatori o come utilizzatori, la sommatoria delle potenze messe in gioco deve essere nulla. Questo teorema è molto utile e potente per cui dedicherà molto spazio alla sua esposizione nella seconda edizione di questo tutorial.
Teorema di Boucherot.
La somma delle potenze attive a reattive fornite dai generatori di una rete corrisponde alle potenze attive dissipate dai componenti resistivi e alla somma delle potenze reattive dissipate dai componenti induttori e condensatori della rete. Si tratta in effetti di un bilancio delle potenze complesse.
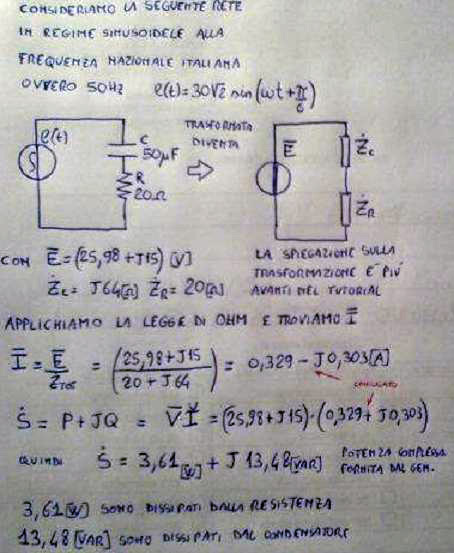
Le freccette in rosso indicano che è stato eseguito il coniugato del numero complesso che rappresenta il fasore di corrente. In questo esempio si è volutamente trascurata la trasformazione da rete reale a rete fasoriale, detta anche simbolica, perché tale spiegazione si trova in un esercizio più avanti in questo tutorial. Spiegarlo ora avrebbe avuto solo l'effetto di distogliere l'attenzione dal teorema che si vuole presentare.
Il metodo delle correnti di maglia.
Consideriamo un circuito elettrico lineare in regime stazionario composto per semplicità di calcolo di sole tre maglie. In tale circuito siano presenti 5 generatori ideali di tensione e 6 resistenze, disposte come in figura.
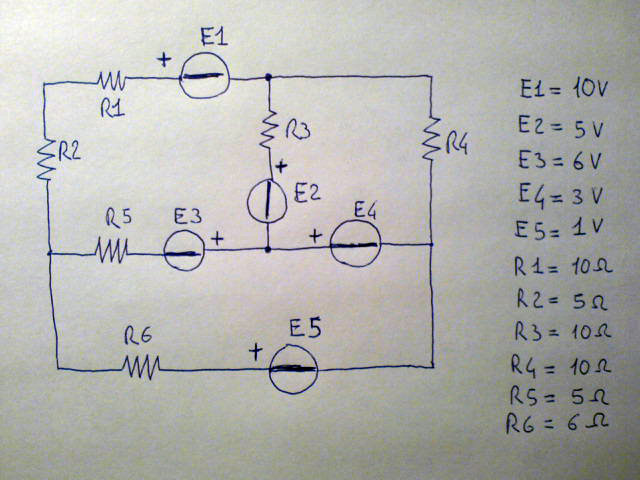
Si scelga ad arbitrio un verso di circolazione per le tre correnti nelle tre maglie. Non è necessario in questo momento ragionare su quale potrà essere il verso reale della corrente, esso resterà definito dai risultati della soluzione del sistema lineare di 3 equazioni (tante quante sono le maglie). Se le correnti risulteranno positive il verso effettivo coincide con quello ipotizzato altrimenti circolano nel verso opposto.
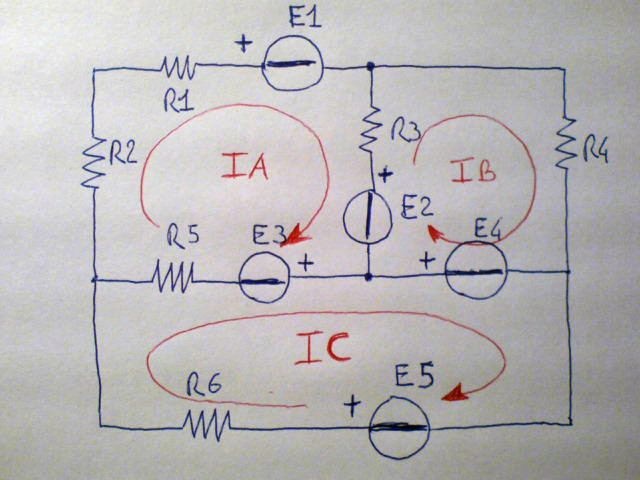
Indichiamo le tre correnti con i nomi IA,IB,IC. Per ogni maglia scriviamo "l'equazione di maglia" che in realtà si tratta di una forma dell'equazione di Kirchhoff per le tensioni in cui ogni caduta resistiva dovrà tenere conto della totalità delle correnti sulla resistenza (legge di Ampere Maxwell). Se ad esempio consideriamo la R3,ci si accorge che la sua caduta di potenziale è pari alla corrente della maglia in esame, meno quella della maglia adiacente, per il valore della resistenza, in effetti si è scritta la legge di ohm.
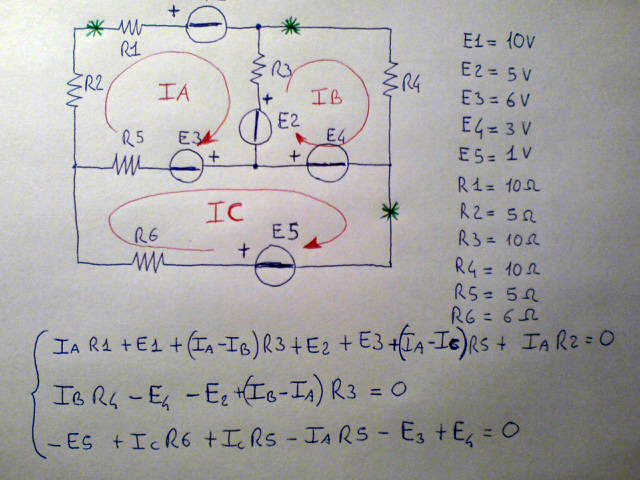
Nell'immagine si vede il sistema lineare che costituisce il modello matematico del circuito. Se non sono stati fatti grossolani errori di incompatibilità del tipo mettere in parallelo due generatori ideali di tensione aventi valori impressi differenti, oppure, dualmente mettere in serie due generatori ideali di corrente avente valore impresso differente, tale modello matematico per il circuito lineare esiste sempre. Attenzione, dato un circuito "compatibile" come quello in figura esiste sempre il suo modello matematico, costituito ad esempio da un sistema lineare, al contrario, dato un sistema lineare "a caso" è quasi impossibile che esso rappresenti un circuito elettrico/elettronico compatibile.
Nell'immagine notiamo degli asterischi verdi, essi costituiscono il punto di partenza per la percorrenza della maglia con l'obbiettivo di ricavare per ognuna una equazione secondo Kirchhoff. Per i principianti diamo questa immagine allegorica: Immaginiamo che i fili del circuito siano i binari di un piccolo trenino elettrico e che i vari componenti, in questo caso solo generatori e resistenze, siano tunnel e stazioni. Prendiamo con le mani la locomotiva del trenino e trasciniamolo lungo il suo binario (la maglia) partiamo dalla stazione centrale, l'asterisco verde, ed ogni volta che entriamo in un "tunnel" ovvero le resistenze scriveremo il valore (IAxR). Questo valore è sempre positivo dato che costituisce una caduta di tensione, il che è equivalente a dire che una resistenza è sempre convenzionata da utilizzatore. Quando il nostro "trenino" entra invece in una "stazione locale" che sarebbe un generatore di tensione, entrerà nell'equazione con il segno della parte in cui si entra nel generatore. Nel caso ci fossero dei generatori reali di corrente vanno prima trasformati in equivalenti generatori reali di tensione spostando la resistenza dal parallelo alla serie e abbinando al generatore di tensione il valore "corrente impressa per il valore della resistenza che posta in parallelo al generatore ideale di corrente.
a questo punto fermiamoci un attimo, e dopo avere stampato le tre immagini sovrastanti, seguiamo con attenzione la prima parte del video tutorial in cui spiego passo passo quanto fatto finora per questo esercizio.
www.gtronic.it/energiaingioco/it/scienza/elettrotecnica/correnti%20di%20maglia%20%281%29%20impostazione%20sistema%2027.09.2007.3gp
Proseguiamo l'esercizio solo se siete sicuri di poter arrivare in maniera autonoma fino a questo punto, quindi, provate a ripartire dal solo schema elettrico, e a ricavare il sistema lineare.
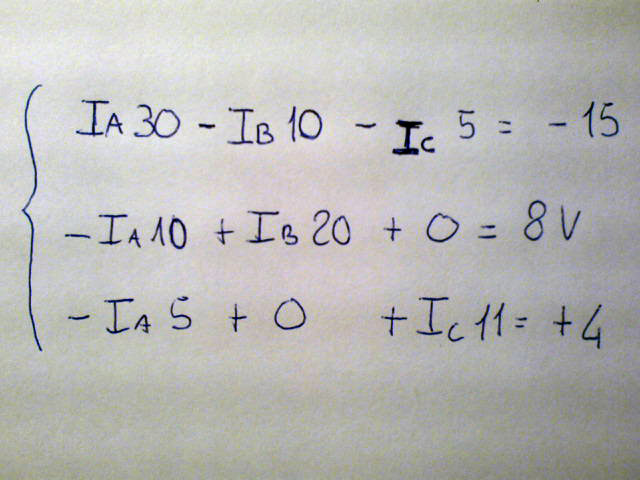
Il sistema lineare va portato in forma normale come si vede nell'immagine. Si ottiene questo risultato eseguendo le moltiplicazione e successivamente eseguendo le somme dei termini omogenei. per omogenei voglio intendere riferiti alla stessa corrente IA,oppure IB, oppure IC. Mettiamo anche un po di ordine, in ogni equazione infatti faremo in modo che la sequenza sia IA, IB, IC seguiti dall'altra parte dell'uguale dal termine noto(ovvero le tensioni). Ricordiamoci che se passiamo da un membro all'altro di un'equazione con un addendo, questo deve cambiare il segno.
Dal sistema così ottenuto estraiamo la matrice dei coefficienti e il vettore dei termini noti (che poi sono i generatori).
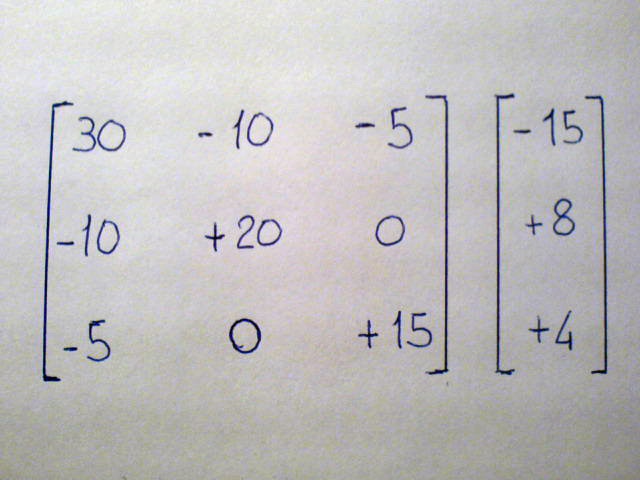
Dal sistema lineare si ricava la matrice associata, questa risulta sempre "quadrata" ed ha delle proprietà che ci possono indicare se la strada intrapresa finora è corretta. È importante coprire i "buchi" lasciati da una variabile (corrente) mancante sommando uno zero. questa procedura è fondamentale per l'inserimento della matrice in dispositivi automatici di calcolo. Noi useremo la calcolatrice sharp perché è la più semplice ed economica in commercio, ma potremo analogamente usare qualsiasi altro prodotto da scuole superiori, ma in questo caso non posso aiutarvi nell'inserimento dei dati e vi invito a leggere il libretto delle istruzioni del vostro calcolatore. Posso comunque assicurare che la procedura sarà molto simile.
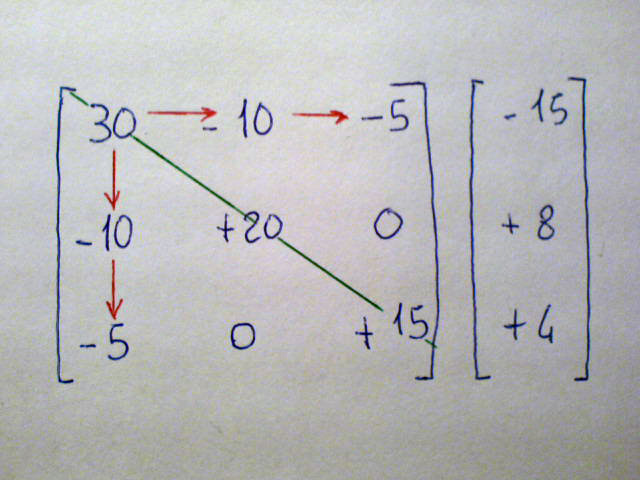
Analizziamo la matrice. La cosa più importante da verificare è che essa sia simmetrica rispetto alla diagonale principale che ho segnato in verde nella foto. Muovendoci verso destra o verso il basso a partire da un elemento della diagonale principale dobbiamo trovare gli stessi coefficienti. Come potete vedere seguendo le frecce rosse. Se questo è vero (come nella foto) allora la matrice è realmente il modello matematico del circuito, se questo non si verifica avete sbagliato qualche calcolo di semplificazione o ordinamento, quindi tornate indietro e rifate i conti fino a che ottenete una matrice simmetrica.
siamo pronti per vedere il secondo tempo del video tutorial, come per il precedente, carte alla mano, seguite il video:
www.gtronic.it/energiaingioco/it/scienza/elettrotecnica/correnti%20di%20maglia%20%282%29%20ricavo%20matrice%2027.09.2007.3gp
A questo punto possiamo inserire la matrice sulla calcolatrice. Questa operazione è differente per ogni tipo di calcolatrice che userete, ma le affinità sono molto spinte. Col la calcolatrice che vedete nella foto si deve richiamare l'algoritmo dei sistemi lineari. Seguiamo questa procedura:
- accendiamo la calcolatrice.
- "mode" -> "6".
- <equation> 1:3-VL (indica che vogliamo impostare un sistema lineare con 3 variabile. premere 1).
- vengono chiesti in sequenza di riga i coefficienti della matrice che daremo con il segno.
- Alla fine in automatico vengono restituiti i valori delle correnti come vediamo nella foto sottostante.
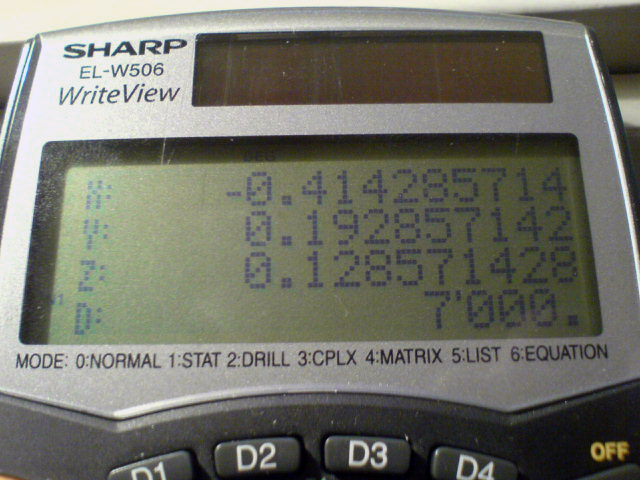
Viene anche fornita una informazione aggiuntiva che per le applicazioni elettriche al momento non ha applicazione. Per pura informazione diciamo che si chiama determinante ed è abbreviato "D".
Gli stessi calcoli possono essere eseguiti a mano svolgendo delle operazioni dette lineari sulla matrice. Le operazioni lineari consistono in moltiplicazioni di tutta la riga per una costante e la somma o differenza di tutta la riga (compreso il termine noto) con un'altra riga del sistema. Lo scopo di eseguire queste operazioni lineari è quello di ottenere un triangolo di zeri sotto la diagonale principale. Una volta ottenuto questo si procede dividendo il termine noto dell'ultima riga (una tensione) per il termine unico rimasto a sinistra dell'uguale della medesima riga (che è una resistenza), di conseguenza otteniamo, come previsto dalla legge di ohm, una corrente, che trovandosi nella colonna di IC è proprio la corrente circolante in quella maglia.
vediamo la terza parte del video tutorial:
www.gtronic.it/energiaingioco/it/scienza/elettrotecnica/correnti%20di%20maglia%20%283%29%20inserire%20calcolatrice%2027.09.2007.3gp
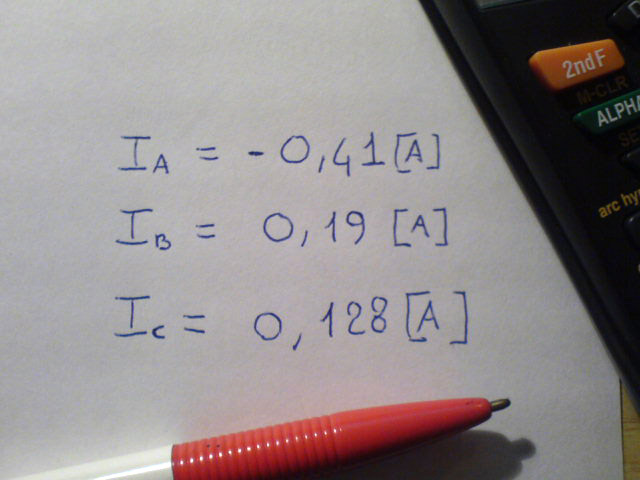
Ecco i risultati ottenuti manualmente, coincidono con quelli fatti al calcolatore. notiamo che la prima corrente è risultata negativa, quindi circola al contrario rispetto al verso ipotizzato all'inizio, le altre due correnti sono invece equiverse. Esiste anche il metodo di studio dei circuiti a più maglie, complementare detto "delle tensioni ai nodi", che poco differisce dalla tecnica esposta ma che necessiterebbe una analoga esposizione. La trattazione diventerebbe davvero troppo prolissa, così ho deciso che lo esporrò in un secondo tutorial, in estensione a questo e solo in funzione della risposta che il presente avrà dalla comunity.
Per testare la comprensione facciamo un esercizio:
prendete il medesimo schema e cambiate a caso tutti i valori delle resistenze e dei generatori. il sistema lineare avrà la stessa forma ma diversi valori numerici come diverso sarà il vettore dei risultati ovvero le tre correnti IA,IB,IC.
Definiamo la reattanza e l'impedenza tramite un chiaro esercizio.
Introduciamo il concetto di reattanza e impedenza eseguendo un esercizio molto ben schematizzato. Seguite prima le foto e la spiegazione per poi ripetere il tutto guidati dal videotutorial.
------------------
Si consideri il circuito in figura alimentato in regime sinusoidale alla frequenza non industriale standard di 95Hz. Questa frequenza è probabilmente generata tramite un convertitore statico, ma il simbolo elettrico rimane il medesimo di un generatore di tensione sinusoidale.
Analizziamo lo schema sottostante, esso si compone del precedentemente detto generatore di tensione sinusoidale, che energizza dei bipoli passivi volutamente connessi di tipologia diversa. Si tratta di un bipolo resistivo in serie con un gruppo induttivo-capacitivo con gli elementi collegati in parallelo.
IL valore della tensione impressa in funzione del tempo del generatore è riportato nell'immagine in cui è presente anche l'informazione della fase iniziale pari a meno 30 gradi.
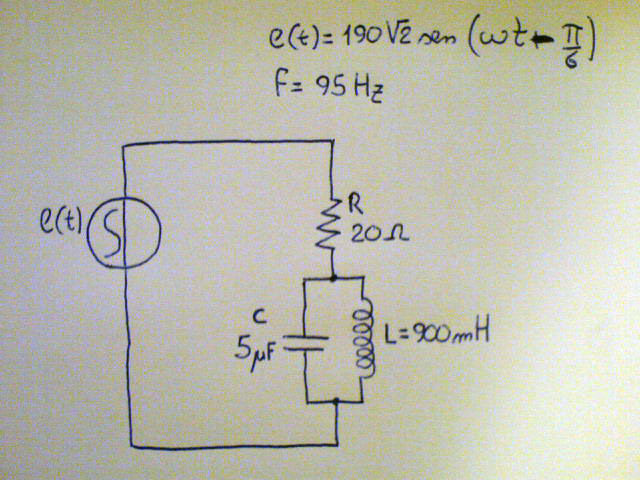
Cominciamo l'esercizio trasformando il generatore dal dominio del tempo al dominio dei fasori, che per noi coinciderà con il piano complesso. La trasformazione non è difficile ma comporta un minimo di ragionamento. Osserviamo come il valore in volt è stato fornito. Dopo la dicitura e(t) ovvero "tensione che varia in funzione del tempo", abbiamo l'uguale seguito da una coppia di numeri, essi sono il valore efficace, che come detto corrisponderà al valore letto dal multimetro digitale (un comune tester) seguito dal coefficiente "radice di due". Quando il generatore viene fornito in questo modalità il tecnico ne ha un vantaggio perché la trasformazione in fasore richiede appunto l'estrazione del valore efficace.
La forma fasoriale, ovvero la trasformata di Stainmentz, richiede di moltiplicare il valore efficace della tensione per il coseno della fase iniziale (in questo caso meno 30 gradi) più il coefficiente dell'immaginario "J" oppure "i" moltiplicato per il seno dello stesso angolo.
L'operazione di conversione è agevolata dalla grafica. Disegniamo la circonferenza goniometrica (si chiama così la circonferenza di raggio unitario in cui si stimano i valori di seno e coseno di un angolo), e riportiamo in essa la fase iniziale di -30°.
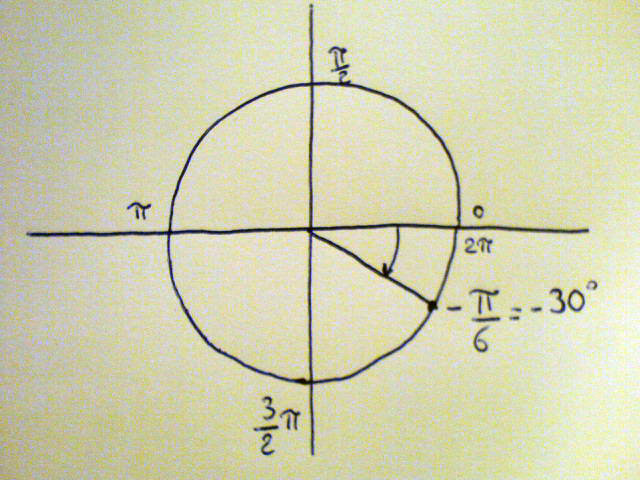
Notiamo che la circonferenza goniometrica è tarata in quarti di Pigreco, corrispondenti all'angolo di 90°. Il raggio riportato a -30°, rappresenta già con buona approssimazione il fasore di tensione V, dato che l'argomento sarà già direttamente riportabile in un diagramma vettoriale. Manca ancora l'informazione relativa al modulo, ovvero la lunghezza del vettore a partire dall'origine degli assi alla punta del fasore.
Proiettiamo il punto di intersezione in ascissa (coseno dell'angolo) e in ordinata (seno dell'angolo).
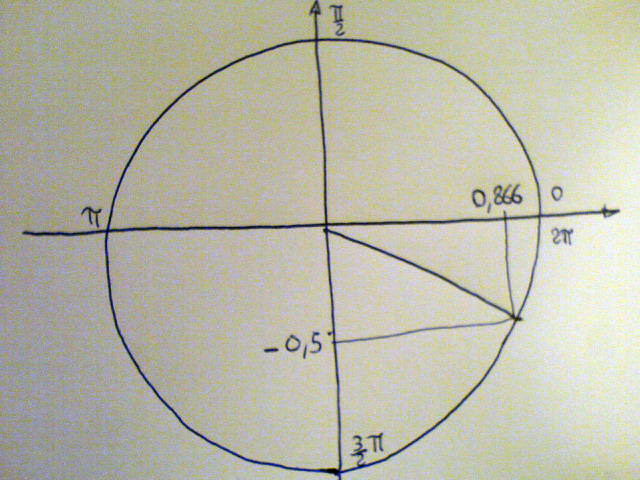
Su questa seconda immagine sono riportate le proiezioni con i loro valori numerici. Ottenere questi valori è molto semplice, basterà digitare in qualunque calcolatrice scientifica "sin-30" e dare invio, anche quella di windows. I neofiti della materia, scopriranno presto che i valori ricorrono spesso quindi dopo un po di esercizio resteranno nella mente rendendo inutile la calcolatrice in questa fase.
Vediamo quali valori si ottengono eseguendo la trasformazione. (prossima immagine) .
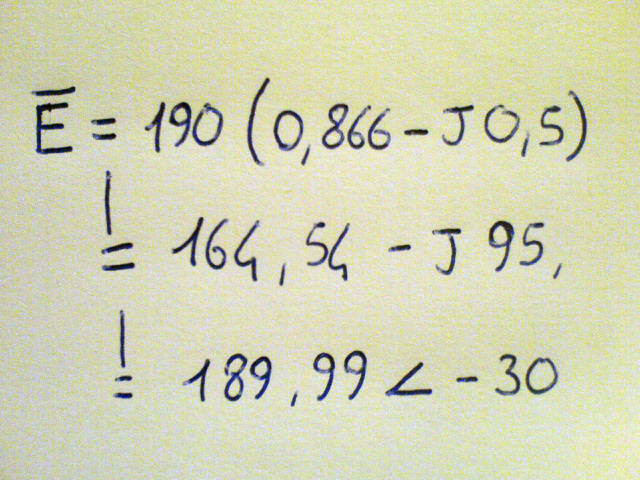
Indichiamo con E il fasore ottenuto, esso si compone del suo valore efficace 190 volt, moltiplicati per il coseno dell'angolo, più "i" o "j" seno del medesimo angolo, nel nostro caso essendo l'angolo negativo compare il segno meno.
Nell'immagine ho omesso l'unità di misura ma ovviamente si tratta di volt.
Nella riga successiva compare compare la rappresentazione in modulo e argomento (fase). tale modalità è ricavabile semplicemente schiacciando un tasto della calcolatrice in praticamente tutti i modelli, ma nel caso si volesse eseguire la conversione a mano tra coordinate cosiddette rettangolari a quelle cosiddette polari o modulo e argomento, allora si dovrà fare, per il modulo, la radice quadrata della somma delle componenti al quadrato, e per l'argomento, l'arco tangente, a volte indicata con tang alla -1, del rapporto della parte immaginaria (quella con il J) con quella reale. Fate una prova e otterrete gli stessi valori visibili in foto.
Una volta convertito il generatore, si procede alla costruzione della "rete simbolica" o rete fasoriale, convertendo i bipoli resistore, condensatore, induttore, nelle corrispettive impedenze. È fondamentale avere chiaro che il valore in Ohm assunto da questi componenti non è una costante legata solo ai valori di resistenza, capacità e induttanza, ma è principalmente legato al valore della frequenza con cui è stimolato il circuito. Ecco perché si farebbe di certo una brutta figura recandosi al negozio per chiedere un "condensatore" da j335 Ohm, come indica nei calcoli visibili nella foto successiva.
Fissiamo nella mente l'importante concetto "reattanza" e "impedenza" pur avendo la stessa unità di misura (ohm) non sono la stessa cosa. La reattanza è un numero reale e rappresenta la reazione del componente alle sollecitazioni periodiche in questo caso sinusoidali, mentre l'impedenza è per definizione un numero complesso composto da una parte reale (la resistenza) e da una parte immaginaria reattiva (j per la reattanza) .

Il procedimento esposto in questa foto segue questo schema:
- Disegno della rete simbolica in cui i bipoli sono rappresentati tutti come rettangolini e il generatore diviene pseudo stazionario, in cui si intuisce che si tratta di un "fasoriale" perché la grandezza impressa E ha sopra il segno di "vettore".
- Si ricava la pulsazione angolare direttamente dalla frequenza. La proporzionalità è molto diretta, vedi calcolo.
- Si ricavano le reattanze induttive e capacitive rispettando la loro definizione.
- Si scrive la definizione generica di impedenza come operatore complesso.
- Si calcolano le tre impedenze, resistiva, induttiva, capacitiva, applicando direttamente la definizione.
- Si riduce la rete a un'unica impedenza (sintesi di impedenze), usando i normali calcoli del regime stazionario dato che la trasformazione in campo complesso ha linearizzato la rete rendendo applicabili tali procedimenti. Ad esempio è ora applicabile la legge di ohm o il calcolo di serie e paralleli di impedenze.
- Applichiamo la legge di ohm, tenendo presente che si tratta di un rapporto tra grandezze complesse, ovvero moltiplichiamo entrambi il numeratore e il denominatore per il complesso coniugato del denominatore.
- Ottenuta la corrente complessa (fasore di corrente in uscita dal generatore), possiamo procedere al calcolo delle potenze fornite dal generatore. Si procede così: S=V*I~. Otterremo una potenza complessa. ovvero composta di una parte reale e una parte immaginaria. Come accennato a glossario, la parte reale è la potenza attiva (si misura in Watt ed è dissipata dalla resistenza), mentre la parte immaginaria, privata del coefficiente "j" è la potenza reattiva (si misura in V.A.R. , volt ampere reattivi e viene dissipata dai componenti reattivi, ovvero la capacità e l'induttore.
Ora lanciamo il videotutorial, e seguiamo passo passo l'esposizione fatta alla lavagna.
http://www.gtronic.it/energiaingioco/it/scienza/elettrotecnica/Regime%20sinusoidale%20lezione%2004.10.07.3gp
Bene, provate ora a fare questo esercizio: usando lo stesso schema cambiate i seguenti parametri: Frequenza delle rete 60Hz, valore della capacità 25uF, valore della induttanza 1000 mH. Calcolate la corrente emessa dal generatore, lo sfasamento tensione corrente (è l'argomento fase tensione meno fase corrente), potenza attiva assorbita dalla rete, potenza reattiva assorbita dalla rete.
Un circuito come quello presentato nell'esercizio può trovare applicazione in elettronica nei filtri passivi, o nelle reti dei filtri attivi costruiti con l'ausilio di operazionali. Reti simili sono usate anche per il rifasamento, li dove non siano impiegate tecniche più robuste come quelle dei "condensatori rotanti" costituiti da motori sincroni di grossa taglia posti in parallelo alla rete e tendenti a mantenere in fase il circuito grazie alle loro proprietà intrinseche.
Filtri passivi e filtri attivi.
La progettazione dei filtri passivi e successivamente attivi non è così complessa come potrebbe sembrare, ma è necessario conoscere la teoria e i concetti di base. In generale è possibile costruire dei filtri passivi utilizzando resistori, condensatori e induttanze opportunamente collegati tra loro. Analizziamo prima il caso più semplice legato alla proprietà dei condensatori di "lasciarsi attraversare" da una corrente, e quindi da un segnale, quando questo ha una frequenza elevata, o di parzializzare il livello del segnale stesso in funzione della sua frequenza. Il concetto così esposto è troppo riduttivo e di certo non accettabile in sede di esame, dato che sembrerebbe che sempre e in ogni caso passi "dall'altra parte del filtro a condensatore" solo la frequenza alta. Questo non è vero, dipenderà infatti da come e dove questo condensatore è collegato. Il condensatore potrebbe infatti essere collegato in modo da deviare verso la massa i segnali ad alta frequenza, lasciando passare nella linea in cui essi sono derivati le basse frequenze. Una spiegazione più approfondita sul funzionamento dei condensatori la ho posta in appendice.
Vediamo le configurazioni di base:
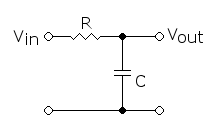
Alle basse frequenze, o addirittura in continua, il condensatore è un circuito aperto per cui il segnale Vin, attraversa la resistenza R, che nel caso fosse successivamente bufferizzata tramite un amplificatore operazionale si trova ad essere equipotenziale, ovvero il segnale non subisce attenuazione (pilotaggio in sola tensione), se invece il filtro viene usato in passivo, ovvero cosi come lo vediamo nella foto, l'attenuazione dovuta alla resistenza sarà proporzionale alla corrente che la attraversa (segnale continuo), all'aumentare della frequenza il condensatore, presentando la sua impedenza, fa da derivatore ohmico portando a massa parte del segnale ch non potrà quindi raggiungere l'uscita. Il diagramma delle attenuazioni di modulo (diagramma di Bode) mostrerà una funzione spezzata costituita da due semirette, la prima sovrapposta alle ascisse e proveniente da meno infinito (riferito alle frequenze), e al seconda, che innesta al punto 1/(R*C), detta frequenza di taglio, a scendere con una pendenza pari a -20db per ogni decade. (vedi diagrammi di Bode).
La seconda configurazione di base è il filtro passa alto, in cui la capacità si trova in serie alla linea del segnale secondo lo schema sottostante:
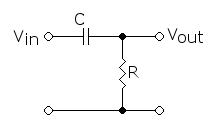
Le basse frequenze incontrano sul loro percorso una capacità che si comporta da circuito aperto (si veda la definizione di reattanza) per cui non potranno attraversare il componente e quindi non raggiungo l'uscita. Le alte frequenze vedono invece un dispositivo quasi trasparente e lo attraversano senza fatica. Entrambi il filtro passa alto e il passa basso, in regime sinusoidale, si presentano come dei partitori variabili con la frequenza in cui, a seconda della posizione a "massa" o al "segnale" del componente reattivo, selezionano la frequenza alta o bassa.
È possibile giocare un po con le configurazioni, ad esempio mettendo in cascata un filtro passa basso a uno passa alto, dopo avere ben tarato le frequenze di taglio che come abbiamo accennato si trovano al valore 1/(R*C), per ottenere un filtro passa banda. analogamente è possibile ottenere filtri rejettori di banda. Condensatori così collegati li troviamo spesso negli stadi di disaccoppiamento della continua dall'alternata degli amplificatori di bassa frequenza, o più propriamente da filtri nei controlli di toni o equalizzatori laddove non siano impiegati, dei sofisticati, se ben ormai comuni, circuiti integrati, progettati per questo scopo. In questo caso vedremo delle capacità collegate semplicemente a dei pin dell'integrato e la questione è risolta dalla circuiteria interna.
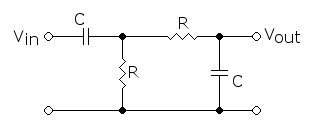
filtro passa banda.
I filtri costruiti con le induttanze, anziché con i condensatori, oppure le combinazioni di grosse induttanze e condensatori li troviamo spesso applicati alla selezione di banda dai inviare agli altoparlanti all'interno dei potenti diffusori acustici e sono noti con il nome di crossover.
Supponiamo di porre queste reti passive dinnanzi a un amplificatore operazionale, sia esso invertente o non invertente ma comunque in retroazione negativa. si ottiene un filtro attivo la cui pendenza di taglio per decade può essere definita dalla configurazione usata.
A causa della prolissità dell'articolo preferisco non esporli ora ma di presentarli alla seconda edizione assieme alle reti correttrici (P.I.D.), e alle configurazione di calcolo integrale, derivativo, logaritmico ed esponenziale degli Amp. OP.
Reti elettriche in regime transitorio.
Vediamo come affrontare lo studio di una rete in regime variabile con l'ausilio delle equazioni differenziali che ne governano l'evoluzione in fase transitoria. Leggete le pagine manoscritte raggiungibili a questo link.
www.gtronic.it/energiaingioco/it/scienza/dispense_pdf/equazioni%20differenziali.pdf
Lo studio dei regimi transitori può comunque risultare piuttosto complicato, quindi è necessario esporre un metodo ben schematizzato che permetta con pochi ragionamenti di essere riadatto ad una moltitudine di casi analoghi. Questo è quanto fatto nelle pagine manoscritte che potrete scaricare dal link sottostante.
www.gtronic.it/energiaingioco/it/scienza/dispense_pdf/studio%20di%20una%20rete%20in%20regime%20variabile.pdf
Concludo questa prima edizione del tutorial "nozioni indispensabili di elettrotecnica" augurando a tutti di avere una buona vita ricca di pace, serenità e soddisfazioni personali.
Marco Gottardo
Appendice di fine pagina: uso della calcolatrice consigliata.
Per omogeneizzare le operazioni in classe normalmente cerco di fare avere a tutti gli allievi una calcolatrice potente ed economica. Al costo di 20€ è disponibile la SHARP EL-506 che garantisce facilità di utilizzo in campo complesso, ovvero nei calcoli fasoriali elettrotecnici. Purtroppo riesce a svolgere sistemi lineari e sistemi in campo complesso al massimo di tre equazioni. Solitamente dimensiono gli esercizi su tre maglie (una maglia una equazione del sistema) ma non tralascio di spiegare la tecnica matriciale (metodo di Gaus) per risolvere i sistemi di ben più di tre equazioni. Queste non saranno mai richieste in sede di esame. Del resto parliamo di scuola superiore dove la dimensione di queste reti elettriche a tre maglie è più che sufficiente.

Vediamo le principali funzionalità specifiche per elettronica/elettrotecnica. Cominciamo con eseguire dei calcoli fasoriali.
esercizio:
Supponiamo che in un circuito sia impressa una tensione fasoriale di V=(30-j15) volt e che l'impedenza complessiva vista alla porta sia di Z=(15-j5) ohm. Vogliamo calcolare la corrente circolante nel circuito, la potenza attiva, la potenza reattiva e la potenza apparente messe in gioco dal generatore.

Come riportato nella figura digitiamo prima il tasto "mode" (risponderà scrivendo sul display "normal stat (spostandoci con la freccia destra corrispondente a F3 compare anche) eqn cplx". sotto a ogni voce c'è un numero da 0 a 3, Noi selezioneremo "3". se in alto a sinistra compare "xy" allora la calcolatrice è commutata in complex mode, ed è pronta a eseguire i calcoli fasoriali.
Procediamo con il calcolo:
- ( 30- "ora guardate sul tasto sopra 8, c'è la "i", schiacciamola, compare i poi 15 e chiudiamo la parentesi)
- cosi facendo avete la tensione fasoriale visualizzata sul display
- digitare il tasto di divisione
- digitare il valore della impedenza (15 - "tasto sopra 8 per i" 5 e chiudete la parentesi ).
- date invio, la calcolatrice risponde visualizzando separatamente la parte reale e la parte immaginaria se è il modello base, visualizza separatamente la parte reale dalla parte immaginaria, mentre la versione write view vi mostrerà contemporaneamente le due parti del valore. Nel primo caso bisognerà digitare il tasto arancione "2ndF" e successivamente "Exp" per visualizzare la parte immaginari. In ogni caso il risultato dovrà essere I=(2.12-i8,13) ovviamente l'unità di misura sarà ampere.
- possiamo visualizzare e anche utilizzare in calcoli successivi la corrente in formato modulo e argomento (detta anche modulo e fase) digitando il tasto arancione "2ndF" seguito da "8" in cui sopra possiamo vedere il simbolo delle coordinate polari. la calcolatrice risponde 8,4 (il modulo) e di nuovo digitando "2ndF" seguito dal tasto "exp" mostrerà la fase in gradi, ovvero -75,38°.
- Calcoliamo la potenza complessa moltiplicando la tensione fasoriale per il complesso coniugato della corrente appena trovata. procediamo (30-i15) per (2.12+i8.13) si ottiene: S=(63,6-i39.93) che posto in modulo e fase è pari a 75 (potenza apparente in volt ampere) con fase -32.12.
- Dal calcolo di S si ottiene direttamente la parte reale (potenza attiva in Watt, pari a 63,6W) e la parte immaginaria (potenza reattiva in V.A.R. volt ampere reattivi, pari a 39,93 V.A.R.)
Il condensatore dal punto di vista elettrotecnico.
Dal punto di vista elettrotecnico il condensatore è costituito da due piastre affacciate (nel caso più semplice) o da forme diverse quali cilindri concentrici o sfere concentriche o semplicemente sfere che trovano la seconda armatura in altre forme attigue o semplicemente a terra.
L'unita di misura è il Farad, ma usualmente sono impiegate porzioni molto piccole di esso in quanto risulta essere una unità di misura piuttosto grande a causa di come è definita.
C= Q/V
dove con Q si indica la totale quantità di carica depositata nell'armatura ed espressa in Coulomb, mentre con V ovviamente la differenza di potenziale elettrico a cui sono sottoposte le piastre.
Il comportamento del componente è assai diverso a seconda del regime di tensione a cui è collegato, in stazionario si comporta infatti come un interruttore aperto, in transitorio risponde al gradino di Heviside con la classica funzione che è la curva di carica che universalmente viene accettato porti il valore della d.d.p. ai capi del condensatore in 4-5 volte la costante di tempo RC che viene a formarsi nel ramo in cui esso è inserito, in sinusoidale assume invece un comportamento ohmico, noto come impedenza capacitiva, che quando puramente detta (non ha cioè altri effetti che infieriscono nel ramo) causa uno sfasamento della tensione in ritardo di Pigreco-mezzi radianti (90°) rispetto alla corrente.
il condensatore costituisce anche un accumulatore di energia elettrostatica nella quantità pari alla metà della capacità per la tensione applicata alla piastre al quadrato.
Se usato in regime stazionario tra le piastre si instaura un campo elettrico (vettoriale) anche esso stazionario. L'operatore differenziale "rotore" ,che esula da questo tutorial, risulta nulla perché se il dielettrico è omogeneo le linee di forza del campo elettrico sono rettilinee, e questo operatore esprime in qualche modo proprio la vorticosità di esse.
La distanza tra le piastre determina l'intensità di questo campo dato che vale la formula:
V=E * h da cui E = V/h con h distanza tra le piastre.
Dato che come detto all'inizio la capacità è inversamente proporzionale alla tensione, essa risulterà anche inversamente proporzionale al campo elettrico secondo la formula, ottenuta per sostituzione:
C =Q/(E*h)
Quindi abbassando il campo elettrico tra le piastre si aumenta la capacità C del dispositivo. Una maniera semplice per ottenere questo scopo è quello di inserire tra le piastre un "dielettrico" più o meno efficace che creando un campo di polarizzazione inverso tra le armature che si andrà a sommare vettorialmente al diretto creato dalle cariche depositate tra di esse avrà appunto l'effetto di diminuire il campo interno complessivo aumentando la capacità, questo a parità di estensione distanza e forma delle armature .
Il condensatore in generale e nelle applicazioni elettroniche.
Il condensatore è un componente elettronico che può immagazzinare una carica elettrica nella stessa maniera spiegata al paragrafo precedente del tutorial. anche un piccolo condensatore per applicazioni elettroniche e di base è costituito da due conduttori che sono separati da un isolante detto dielettrico (carta, plastica, ceramica...). Hanno forme molto diverse solitamente sono dei cilindretti verticali orizzontali, sono costruiti arrotolando due lamine di conduttori isolate dal dielettrico, oppure hanno forma di goccia o bottoncino e sono costituiti da una o più facce metalliche immerse nel dielettrico e collegate in parallelo. La capacità del condensatore si misura in Farad. Oltre alla pila, il condensatore è l'unico dispositivo elettronico che può immagazzinare energia elettrostatica, sotto forma di tensione ma contrariamente alla pila rilascia la sua carica in maniera istantanea o controllata da un carico resistivo, per questo viene usato nei flash delle macchine fotografiche. I condensatori possono essere fissi o variabili quelli fissi a loro volta possono essere normali oppure elettrolitici. I condensatori elettrolitici funzionano esattamente come quelli normali ma poiché il materiale isolante è costituito da un elettrolita hanno una polarità, il piedino polarizzato viene indicato con una freccia o un segno sul corpo del condensatore se non viene rispettata durante il montaggio del condensatore sul circuito questo verrà danneggiato irreparabilmente.
I condensatori variabili sono costituiti da alette di metallo separate da un dielettrico fatto di lamine isolanti o dall’aria. Un classico impiego è la sintonia delle vecchie radio, quelle con la rotella per cercare le stazioni, in questo caso il condensatore è fatto da alette a forma di mezzaluna saldate a pettine su un asse, una serie di queste rimane fissa e un’altra ruota, la capacità varia a seconda di quanta superficie si sovrappone.
I più comuni condensatori sono:
- Ceramici
- Poliestere
- Elettrolitici
- Tantalio
Condensatori ceramici
I condensatori ceramici da 10 fino ad 82 picofarad sono siglati con due cifre pertanto la loro lettura è semplice ed immediata.
Per i valori compresi tra 1 e 8.2 le case costruttrici usano il punto, cioè scrivono 1.2 - 1.5 - 1.8 oppure mettono tra le due cifre la lettera p ( che sta ad indicare picofarad ) quindi 1p2 - 1p5 - 1p8 con significato ad esempio di 1 picofarad e 8.
Le prime difficoltà di lettura arrivano con le capacità che superano i 100 picofarad dato che le diverse case costruttrici impiegano una propria modalità di stampigliatura.
Il Metodo giapponese: di stampigliare i condensatori ceramici consiste nell’indicare con le prime due cifre la capacità e con la terza il numero degli zeri da aggiungere, quindi i condensatori da 100 -120 - 150 picofarad sono siglati 101 - 121 - 151.
Ovviamente nel caso di condensatori contrassegnati con due dopo le cifre significative verranno aggiunti due zeri, quindi 102 -122 - 152 corrispondono a condensatori di 1000 - 1200 - 1500 picofarad.
Se troveremo dei condensatori siglati 103 - 123 - 153, alle prime due cifre dovremo aggiungere 3 zeri, quindi:
10 + 000 = 10.000 picoFarad
2 + 000 = 12.000 picoFarad
15 + 000 = 15.000 picoFarad.
Altre Case siglano il condensatore in nanoFarad aggiungendo dopo il numero la lettera minuscola n.
Ai condensatori siglati 1n - 10n -100n, per ottenere il corrispondente valore in picoFarad dovremo aggiungere tre zeri, quindi:
1 + 000 = 1.000 picoFarad
10 + 000 = 10.000 picoFarad
100 + 000 = 100.000 picoFarad.
Poiché da 1.000 pF fino a 8.200 pF abbiamo anche valori di 1.200 -1.800 - 2.200 - 3.300 - 4.700 - 5.600 - 6.800 - 8.200 pF, troveremo che la lettera n viene in questi casi interposta tra la prima e la seconda cifra al posto del punto, pertanto i condensatori siglati 1n2- 1n5 - 3n3 - 4n7 avranno una capacità di 1.200 - 1.500 - 3.300 - 4.700 picoFarad.
Altre Case preferiscono siglare la capacità in microFarad, ma poiché non sempre sul corpo dei condensatori vi è lo spazio per stampigliare numeri con molte cifre, si esclude il primo zero e in luogo della virgola si utilizza il punto, perciò i condensatori siglati .1 - .01 avranno queste capacità:
.1 = 100.000 pF
.01 = 10.000 pF
Condensatori al poliestere
I condensatori al poliestere oltre ad essere siglati con uno dei due sistemi descritti per i condensatori ceramici, possono utilizzare anche la lettera greca u (micro). In pratica la lettera u sostituisce lo 0,(zero virgola), quindi un condensatore siglato u01 avrà una capacità di 0,01 microFarad.
Perciò se abbiamo dei condensatori siglati u1 - u47 - u82, dovremo leggerli 0,1 - 0,47 - 0,82 microFarad.
Sempre sui condensatori in poliestere, oltre al valore della capacità vengono riportati dei numeri o altre sigle che possono trarre in inganno un principiante.
Ad esempio 1K potrebbe essere facilmente interpretato come 1 Kilo, cioè 1.000 picoFarad, perché la lettera K viene considerata erroneamente l'equivalente a 1.000, mentre la reale capacità di questo condensatore è di 1 microFarad.
La lettera M, ad esempio 1M, potrebbe essere considerata l'equivalente di microFarad, mentre in realtà le lettere M - K - J presenti dopo il valore della capacità indicano solo la tolleranza:
M = tolleranza minore del 20%
K = tolleranza minore del 10%
J = tolleranza minore del 5%
Quindi un condensatore siglato .01M indica che il condensatore è da 10.000 pF con una tolleranza minore del 20%.
Faccio presente che la maggior parte dei condensatori reperibili in commercio hanno una tolleranza del 20%.
Tolleranze minori del 5% non sono facili da reperire e quando si trovano hanno costi notevolmente elevati.
Preciso che un condensatore siglato con una tolleranza del 20% non significa che abbia uno scarto di capacita del 20% rispetto al valore riportato sull'involucro.
Posso anzi dirvi che quasi sempre questi condensatori hanno tolleranze notevolmente inferiori.
Infatti le Case Costruttrici usando la sigla M assicurano che la capacità non supererà mai il 20% del valore riportato sull'involucro del condensatore, quindi non si può escludere che questa possa risultare anche solo del 7% - 10% - 12% ecc.
Dopo le lettere M - K - J indicanti la tolleranza, sono presenti dei numeri che stanno ad indicare la tensione di lavoro.
Quindi se troverete scritto .15M50 significa che il condensatore ha una capacità di 150.000 picoFarad, che la sua tolleranza è M = 20% e la sua tensione di lavoro è di 50 volt.
Se trovate scritto .1K100 significa che il condensatore ha una capacità di 100.000 picoFarad, che la sua tolleranza è K = 10% e la sua tensione di lavoro è di 100 volt.
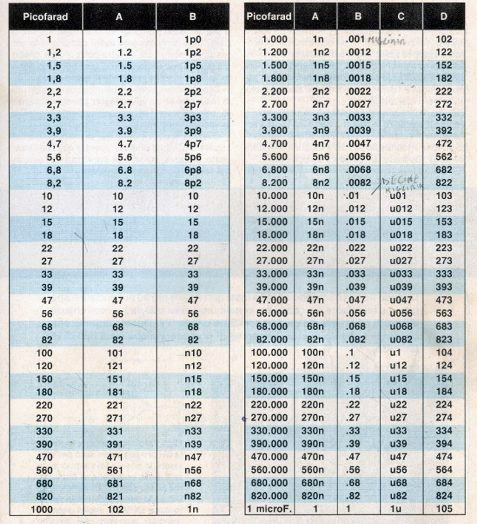
Questa utile tabella la ho presa da una vecchia rivista, la uso a scuola con i miei studenti 14-enni. è semplice e pratica da usare.
Condensatori ceramici (parte sinistra della tabella)
Nella prima colonna il valore della capacità come può risultare stampato sul corpo del
condensatore se espresso in "picofarad". Nella seconda colonna il valore espresso secondo il
codice giapponese, in cui la terza cifra indica quanti ZERI occorre aggiungere dopo i due primi numeri. Nella terza colonna B si noterà che la lettera "p" posta tra due numeri equivale ad una virgola.
Condensatori poliestere ( parte destra della tabella)
Nella prima colonna, il valore di capacità espressa in "picofarad", mentre nelle altre colonne indicate A-B-C-D, come queste capacità possono venire stampigliate sul corpo dei condensatore. Su questi condensatori le lettere K-M-J poste dopo il numero indicano la TOLLERANZA seguita dalla tensione di
lavoro. Nella colonna A si noterà che la lettera "n" posta tra due numeri , equivale ad una virgola.
Vediamo un esempio di lettura della capacità del condensatore al poliestere.
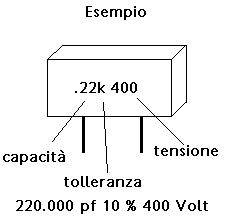
Nella seconda edizione verranno presentate le induttanze.














